Ford Fulkerson Algorithm for Maximum Flow Problem

Introduction

When a Graph Represent a Flow Network where every edge has a capacity. Also given that two vertices, source 's' and sink 't' in the graph, we can find the maximum possible flow from s to t with having following constraints:

1. Flow on an edge doesn't exceed the given edge capacity
2. Incoming flow is equal to Outgoing flow for every vertex excluding sink and source

Algorithm

1. Start with f(e) = 0 for all edge e ∈ E.
2. Find an augmenting path P in the residual graph Gf .
3. Augment flow along path P.
4. Repeat until you get stuck.

Example

Consider the following graph

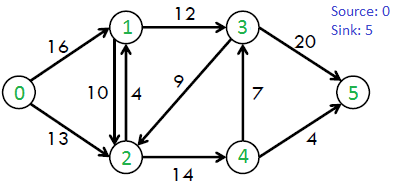
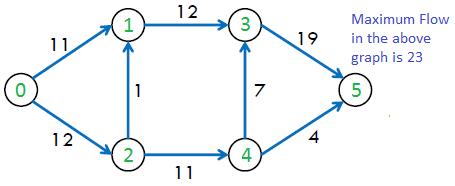
Maximum possible flow in the given graph is 23

var fordFulkerson = require('graph-theory-ford-fulkerson');

var graph = [  
    [ 0, 16,  13, 0,  0,  0 ],
    [ 0,  0, 10, 12,  0,  0 ],
    [ 0,  4,  0,  0, 14,  0 ],
    [ 0,  0,  9,  0,  0, 20 ],
    [ 0,  0,  0,  7,  0,  4 ],
    [ 0,  0,  0,  0,  0,  0 ]
];

console.log("The maximum possible flow is " +  
    fordFulkerson(graph, 0, 5));

Usage

require('graph-theory-ford-fulkerson')( graph, source, sink )

Compute the maximum flow in a flow network between source node sourceand sink node sink.

Arguments: - graph: The Graph which representing the flow network - source: source vertex - sink: sink vertex

Returns: Returns a number representing the maximum flow.

Installation

npm install graph-theory-ford-fulkerson

License

© 2016 Prabod Rathnayaka. MIT License.

Get on Github